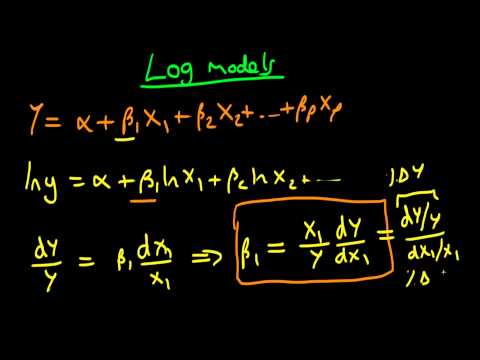What Form 8865 Functional 2024

Hi there, in this video, I wanted to talk about the interpretation of regression results in the context of log models. In the last video, we looked at the interpretation of individual coefficients in a regression equation of the form y = alpha + beta1*X1 + beta2*X2 + ... + betaP*XP. We discussed how the individual beta coefficients represent the marginal effect of each variable on the dependent variable. Specifically, if X1 were to increase by 1 unit, holding all other variables constant, we looked at what happens to the dependent variable. Now, let's consider a scenario where we regress log Y on the logs of our independent variables. In this case, the equation becomes beta1*log(X1) + beta2*log(X2) + ... + betaP*log(XP). What do these individual beta coefficients represent? Well, we can still think about them in similar terms as we did in linear regression, but the interpretation is slightly different. In this context, the beta coefficients represent the corresponding increase in log Y if log X1 were to increase by 1 unit. To give a more concise explanation, let's find the differential of both sides of the equation: dy/Y = beta1*dX1/X1 (assuming all other variables are constant). Rearranging this equation, we get an expression for beta1: beta1 = (X1/Y)*(dy/dX1). In economics, we often express this in terms of elasticity, which can be written as the change in Y divided by Y, divided by the change in X1 divided by X1. In other words, beta1 represents the partial elasticity of the dependent variable with respect to X1, assuming all other variables are constant. It measures the percentage increase in Y from a 1% increase in X1. Now, let's consider a different scenario where we have a log-dependent variable, but non-logged independent variables: log Y = alpha + beta1*X1 + ... + betaP*XP....