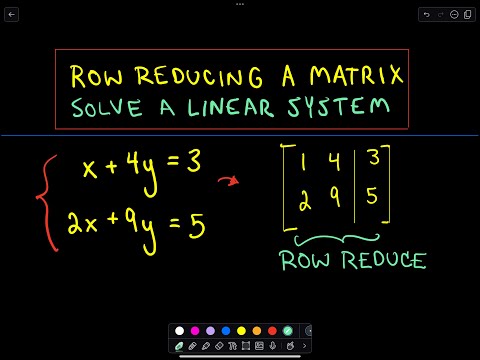
All right, in this video, I'm going to start talking about solving linear systems of equations using matrices. So, a little bit before we get started, some notation: this relates to R subscript I and the little arrows in between rows of J. What that means is we're going to switch the Ith row and the Jth row. There's another rule that says you can multiply any row by a constant and just replace that row. So, that's what this second notation is going to mean. And then the last one says you can add or equivalently subtract rows and replace a certain row. Okay, so that's what's going on there. And in general, we're going to have a system of equations that we're trying to solve. The goal is we want to make it look basically something like this. Okay, so I'm going to put some stuff on the left side, some stuff on the right side. This will make more sense in a second. You basically want ones going down the diagonal and zeros everywhere else. And what this means is your system of equations is going to have a unique solution. You know, there's cases, if you've done elimination by addition or substitution, sometimes you find that there's no solutions or that there's infinitely many solutions, and that can happen as well. There's going to be infinitely many solutions if one of your rows ends up becoming equal, and then on the right side of the bar, you'll find out that there's no solutions if you end up with a number on the left side. I should be careful. We'll come back to this in a different video. It's probably easier, so just to start off with, let's solve this first linear system of equations. And notice,...
Award-winning PDF software





Video instructions and help with filling out and completing When Form 8865 Reduction